Transformaciones Geométricas
2.1. Transformaciones bidimensionales.
Las transformaciones nos
permiten alterar de una forma uniforme toda la imagen. Es un hecho que a
veces es más fácil modificar toda la imagen que una porción de ella.
Esto supone un complemento muy útil para las técnicas de dibujo manual,
donde es normalmente más fácil modificar una pequeña porción del dibujo
que crear un dibujo completamente nuevo.
Se aplica una traslación en un objeto para cambiar su
posición a lo largo de la trayectoria de una línea recta de una dirección de
coordenadas a otra. Convertimos un punto bidimensional al agregar las
distancias de traslación, tx y ty la posición de coordenadas original (x,y)
El par de distancia de traslación se llama vector de
traslación o vector de cambio. Se pueden expresar las ecuaciones anteriores en
una sola ecuación matricial al utilizar vectores de columna para representar
las posiciones de coordenadas y el vector de traslación
Los polígonos se trasladan al sumar el vector de traslación
a la posición decoordenadas de cada vértice y se vuelve a generar el polígono
utilizando un nuevo conjuntode coordenadas y vértices y las especificaciones
actuales de los atributos.
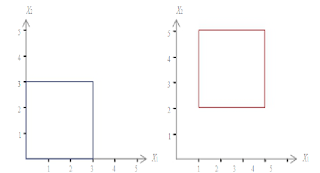
Esta transformación goemétrica se usa para mover un objetoo grupo de objetos alrededor de un punto.
Como puedes observar, los vectores que unen
cada punto de la figura 1 con sus transformados de la figura 2 (AA',
BB', CC')
tienen el mismo módulo, la misma dirección y el mismo sentido. Además, la figura 2
tiene la misma forma y el mismo tamaño que la figura 1. A este movimiento se le llama traslación de vector v, siendo v
el vector libre definido por cualquiera de los vectores anteriores.
2.1.3 Rotación.
Se aplica una rotación bidimensional en un objeto al cambiar
su posición a lo largo de la trayectoria de una circunferencia en el plano de xy
. Para generar una rotación, especificamos un ángulo de rotación θ y la
posición (x r , y r ) del punto de rotación (o punto pivote) en torno al cual
se gira el objeto.
2.1.3 Escalación.
Una transformación de escalación altera el tamaño de un
objeto. Se puede realizar esta operación para polígonos al multiplicar los
valores de coordenadas (x, y) de cada vértice por los factores de escalación s x
y s y para producir las coordenadas
transformadas (x’, y’ ). Permite cambiar el tamaño de un objeto expandiéndolo o
contrayéndolo en sus dimensiones.
2.2 Coordenadas homogéneas y representación matricial.
En este
tema consideramos cómo se pueden volver a formular lasrepresentaciones de la matriz de modo que se pueden procesar de manera
eficiente esassecuencias de transformación.Es posible expresar cada una
de las transformaciones básicas en la forma de matrizgeneral con las posiciones de coordenadas P y P’ representadas como
columnas de vector.
P' = M1· P + M2
La matriz
M1 es una matriz de 2 por 2 que contiene factores de multiplicación y M2 esuna
matriz de columnas de dos elementos que contiene términos de traslación. Para
latraslación, M1es la matriz de identidad. Para la rotación o la escalación M2 contiene
lostérminos de traslación asociados con el punto pivote o el punto fijo de
escalación.
Las representaciones de matriz o
representaciones matriciales son métodos estándarpara implementar transformaciones en sistemas de gráficas. En muchos sistemas, lasfunciones de rotación y escalación producen transformaciones con respecto
del origen delas coordenadas.
2.3 Composición de transformaciones bidimensionales.
La formación de productos con las matrices de transformación
a menudo se le conoce como concatenación o composición de matrices. Entonces se
puede decir, que una transformación compuesta bidimensional es una secuencia de
transformaciones, una tras otra.
Traslaciones.
Se aplican dos vectores de traslación sucesivos ( tx1, ty1) y
( tx2, ty2) en la posiciónde coordenadas P, la
localización transformada final P, la localización transformada final P’se
calcula como:
P’ = T (tx2, ty2).{ T ( tx1,
ty1 ).P} = {T (tx2, ty2).T(tx1, ty1)}.P
donde se representan P y P’ como vectores de
columna de coordenadas homogéneas.Podemos
verificar este resultado al calcular el producto de la matriz para las dosagrupaciones asociativas. Asimismo, la matriz de
transformación compuesta para estasecuencia
de transformaciones es:
Rotaciones.
Dos
rotaciones sucesivas que se aplican en el punto P producen la posicióntransformada
P' = R ( θ2
)· {R ( θ1 ).P} = {R ( θ2 ). R ( θ1 )}.P
Al
multiplicar las dos matrices de rotación, podemos verificar que dos
rotacionessucesivas son aditivas:
R ( θ2 )· {R ( θ1 ) = R ( θ2 + θ1
)
de modo que es posible calcular las
coordenadas giradas finales con la matriz derotación compuesta como:
P' = R ( θ2 + θ1
).P
Escalaciones.
Concatenar matrices de
transformación para dos operaciones de escalación sucesivasproduce
la siguiente matriz de escalación compuesta:
La matriz
resultante en este caso indica que las operaciones de escalación sucesivasson multiplicativas. Es decir, si debiéramos
triplicar el tamaño de un objeto dos veces enuna sucesión, el tamaño
final sería nueve veces el tamaño original.
2.3.2Rotación del punto pivote general
Con un
paquete gráfico que sólo ofrezca una función de rotación para girar objetoscon
respecto del origen de las coordenadas, podemos generar casi cualquier punto
pivoteseleccionado ( xr, yr ) al realizar la
siguiente secuencia de operaciones de traslación-rotación-traslación:
1.Traslade el objeto de modo que se mueva la posición del punto pivote al
origende las
coordenadas.
2.Gire el objeto con respecto del origen de las coordenadas
3.Traslade el objeto de manera que se regrese el punto pivote a su posiciónoriginal.
2.3.3 Escalacion del Punto Fijo General
Una
transformación de escalación altera el tamaño de un objeto. Se puede
realizar esta operación para polígonos al multiplicar los valores de
coordenadas (x,y) de cada vértice por los factores de escalación sx y sy
para producir las coordenadas transformadas (x' , y').
El
factor de escalación sx escala objetos en la dirección de x, mientras
que el factor de escalación sy lo hace en la dirección de y.
Cuando
se asignan el mismo valor a sx y sy' se general una escala uniforme. Y
cuando se asignan valores distintos a sx y sy se obtiene un escala
diferencial.
Podemos
encontrar la localización de un objeto escalonado al seleccionar una
posición llamada punto fijo, que debe permanecer sin cambio después de
la transformación de escalación.
La figura ilustra una secuencia
de transformación para producir escalación con respecto de una posición fija
seleccionada (xf, yf) al utilizar una función de
escalación que sólo puede escalar en relación con el origen de las coordenadas.
1.Traslade el objeto de modo que
el punto fijo conincida con el origen de las coordenadas.
2.Escale el objeto con respecto
del origen de las coordenadas.
3.Utilice la traslación inversa
del paso 1 para regresar el objeto a su posición original.
2.3.4 Propiedades de concatenación
La
multiplicación de matrices es asociativa. Para tres matrices
cualesquiera A, B y C, el producto matricial A·B·C se puede llevar a
cabo al multiplicar primero a por B o multiplicar primero B por C:
A*B*C=(A*B)*C=A(B*C)
Por
tanto, podemos evaluar los productos matriciales al utilizar una
agrupación asociativa ya sea de izquierda a derecha o de derecha a
izquierda.Por otro lado, los productos de la transformación tal vez no
sean conmutativos. En general el producto matricial A·B no es igual que
B·A. Esto significa queremos trasladar y girar un objeto, se debe tener
cuidado sobre el sentido en que se evalúa la matrizcompuesta.

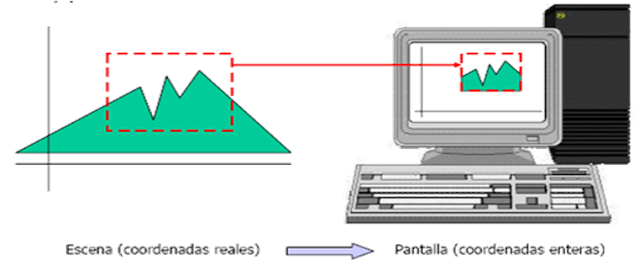
2.4 Transformación ventana-área de vista
Consideremos que tenemos una ventana del mundo real cuyos límites son {x_min, x_max, y_min, y_max}
Deseamos mapear a coordenadas de pantalla con límites {u_min, u_max, v_min, v_max}. Para tal propósito debemos :
1.- Trasladar las coordenadas mínimas al origen T(-x_min, -y_min),
2.- Aplicar un escalamiento anisotrópico dado por S((u_max-u_min)/(x_max-x_min), (v_max-v_min)/(y_max-y_min)) y
3.- Trasladar las coordenadas a un nuevo origen u_min, v_min T(u_min, v_min)
Esta correspondencia se puede
efectuar si el programador de la aplicación proporcionaal paquete gráfico una matriz de
transformación para la correspondencia. Otra forma es queel programador de la aplicación especifique una
región rectangular en coordenadas demundo,
llamada ventana de coordenadas mundiales y una región rectangularcorrespondiente en coordenadas de pantalla, llamada área de vista, con la cual
se establecela
correspondencia de la ventana de coordenadas mundiales. La transformación queestablece la correspondencia entre la-ventana y el
área de vista se aplica a todas lasprimitivas
de salida en coordenadas de mundo para que correspondan a coordenadas depantalla.
Una transformación bidimensional
general, que representa una combinación de traslaciones, rotaciones y
escalaciones, se puede expresar como:
Los cuatro elementos rsij
son los términos multiplicativos de rotación-escalación en la transformación
que implican sólo ángulos de rotación y factores de escalación. Los elementos
trsx y trsy son los términos de traslación que contienen
combinaciones de distancias de traslación, coordenadas de punto pivote y de
punto fijo, así como de ángulos de rotación y parámetros de escalación. Por
ejemplo, si se debe escalar y girar un objeto con respecto de las coordenadas
de su centroide (xc, yc) y después trasladarlo, los
valores para los elementos de la matriz de transformación compuesta son:
T
(tx, ty) · R (xc, yc, ө) · S (xc, yc,
sx, sy)
2.6 Representacion Matricial de Transformaciones Tridimensionales.
Las
transformaciones geométricas tridimensionales permiten construir
escenarios en tres dimensiones a partir de primitivas geométricas
simples (esfera, cubo, cono, cilindro, etc). En concreto, las
transformaciones de traslación, escalado y rotación son indispensables
para esta
tarea y constituyen un punto muy importante en en la materia.
El
tema pretende mostrar una traslación, un escalado o una rotación sobre
una primitiva geométrica en tres dimensiones. Por ejemplo, si se desea
hacer algo tan simple como girar un cubo un ángulo dado alrededor de un
eje de coordenadas resulta muy complicado de explicar mediante dibujos
2D que sólo muestren la situación inicial y final del cubo, y que no
muestran como el cubo sufre dicha transformación y porqué la situación
final es la que es.
Las transformaciones geométricas 3D que se estudian son tres en concreto: traslación,escalado y rotación.
•
Traslación. Consiste en desplazar un objeto a una nueva posición. Las
nuevas coordenadas se obtienen mediante las siguientes ecuaciones:
− x’= x+Tx
− y’= y+Ty
− z’= z+Tz
donde (Tx, Ty, Tz) son los factores de traslación
• Escalado. Consiste en cambiar el tamaño de un objeto. Las nuevas coordenadas se obtienen mediante las siguientes ecuaciones:
− x’= x Sx
− y’= y Sy
− z’= z Sz
donde (Sx, Sy, Sz) son los factores de escalado
•
Rotación. Consiste en girar un objeto alrededor de uno de los ejes de
coordenadas. Respecto al eje Z, por ejemplo, las nuevas coordenadas se
obtienen mediante las siguientes ecuaciones:
− x’= x cos(α)- y sen(α)
− y’= x sen(α)+ y cos(α)
− z’= z
donde α es el angulo de giro
Composición de transformaciones 3D. Hay
transformaciones que no se pueden considerar mediante transformaciones
complejas. Para ello se divide el problema complejo en subproblemas más
simples. También se puede resorber directamente a partir de las
propiedades de las matrices ortogonales.
Nodo Transform.
Por
defecto todos los objetos son creados en el centro del escenario de
realidad virtual. El primer paso es conocer el sistema de coordenadas
usado por el lenguaje, para poder colocar un objeto en otro punto.
En VRML tenemos:
|
Un
mundo virtual tiene su sistema de coordenadas situado en el centro. Con
el nodo Transform, se determina un nuevo sistema de coordenadas para un
grupo de objetos.
Este
nuevo sistema de coordenadas sufre unas transformaciones: puede ser
trasladado a un punto determinado, puede ser girado un determinado
ángulo y puede tener una escala distinta a la original. El grupo de
objetos especificados en el nodo sufrirán las mismas transformaciones,
es decir, serán trasladados, girados y variados de escala.
La estructura general del nodo Transform es:
Transform{
translation x y z
rotation x y z Radianes
scale x y z
children[
]
}
En este nodo nos encontramos los campos de translación, rotación y escala. El campo children,
es donde se especifican los objetos que sufrirán esas transformaciones.
No es necesario que estén los tres términos en una transformación.
Para realizar translaciones en VRML, podemos realizarlas con el campo translation. Este campo permite indicar la posición a la cual colocamos el sistema de coordenadas perteneciente al objeto o grupo de objetos.
La estructura de este campo es:
|
Transform{
translation x y z
children[
]
}
|
X = distancia del desplazamiento en el eje x.
Y = distancia del desplazamiento en el eje y.
Z = distancia del desplazamiento en el eje z.
|


Cual es la fuente de esta información?
ResponderEliminarTu Pinga xD
Eliminar